A Proof of Descartes' Circle Theorem
(concerning four circles, each of which touches the remaining three)
Suppose four circles lying in a plane, such that any two of them touch each other externally (meaning that in each pair of touching circles each centre is external to the other circle of the pair). If the centres of a pair are P, Q, then the point of tangency lies on the line PQ, and the length PQ is equal to the sum of the radii. So if P, Q, R, S are the centres of the four circles, and a, b, c, d are their radii, we have the six equations
\[ \dpi{100} PQ = a + b \qquad QR = b+c \qquad RP= c+a \] \[ \dpi{100} PS = a+d \qquad QS = b+d \qquad RS = c+d. \]
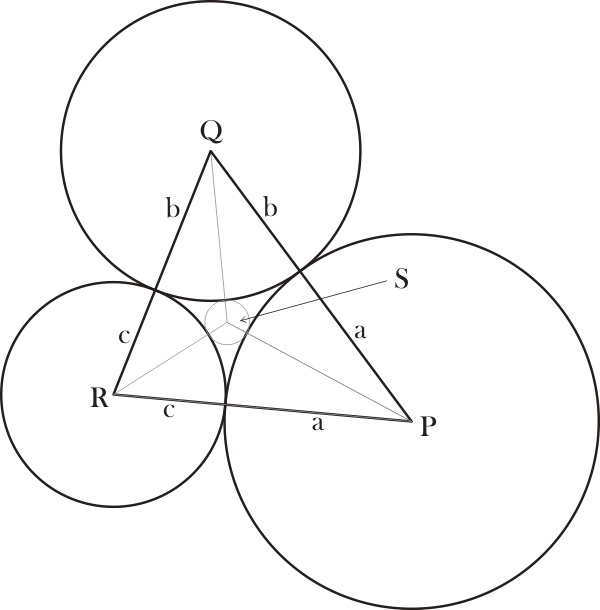
Figure1
Descartes' Circle Theorem states that in such a situation a,b,c,d are related by the equation
\[ 2(\frac{1}{{d}^{2}}+\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}+\frac{1}{{c}^{2}}) = {\left(\frac{1}{d}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)}^{2} \]
We give a simple proof using trigonometry and a fair bit of algebra. For definiteness, suppose that S is inside the triangle PQR and let
\[ \theta = \mbox{angle} \; PSQ \qquad \phi = \; \mbox{angle} \; QSR \qquad \psi = \; \mbox{angle} \; RSP \]
then
\[ \theta + \phi + \psi = 2\pi. \]
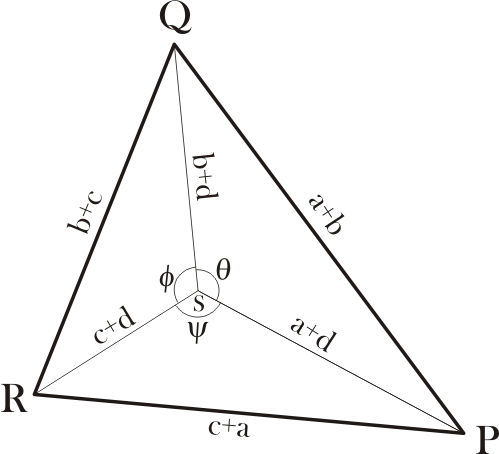
Figure2
By the cosine rule, applied to the triangle PSQ,
\[ (a+b)^{2} = (a+d)^{2} + (b+d)^{2} - 2(a+d)(b+d)\;cos(\theta) \] \[ \therefore cos(\theta) = \frac{2d^{2} + 2ad + 2bd -2ab}{ 2(a+d)(b+d) } = \frac{AB - 2ab}{AB} = 1 - \frac{2ab}{AB} \]
where we have written A for a+d, B for b+d. Hence
\[ s = sin(\theta/2) = \sqrt{\frac{1-cos(\theta)}{2}} = \sqrt {\frac{ab}{AB}} = \sqrt{\alpha\beta} \]
where we have written α for a/A and β for b/B. In just the same way, we obtain
\[ t = sin(\phi/2) = \sqrt {\frac{bc}{BC}} = \sqrt{\beta\gamma} \] \[ u = sin(\psi/2) = \sqrt {\frac{ca}{CA}} = \sqrt{\gamma\alpha} \]
where we have also set C = c+d and γ = c/C.
Now, the fact that the angles θ/2 φ/2 and ψ/2 add up to π implies that their sines have a certain relationship, we which now proceed to elucidate. We have:
\[s = sin(\theta/2) = sin(\pi - \phi/2 - \psi/2) = sin (\frac{\phi+\psi}{2}) \] \[ = sin(\phi/2)cos(\psi/2) + cos(\phi/2)sin(\psi/2) \] \[ = t \sqrt{1-u^{2}} + u \sqrt{1-t^{2}} \].
This relates s, t and u; but the equation is ugly. It can be improved by getting rid of the square roots. Squaring both sides of the equation:
\[ s^{2} = t^{2}(1-u^{2})+(1-t^{2})u^{2} + 2tu \sqrt{(1-t^{2})(1-u^{2})} \] \[ \therefore (s^{2} - t^{2} - u^{2} +2t^{2}u^{2})^{2} = 4t^{2}u^{2}(1-t^{2})(1-u^{2}) \] \[ \therefore s^{4} + t^{4} + u^{4} + 4t^{4}u^{4} - 2s^{2}t^{2} - 2s^{2}u^{2} + 4s^{2}t^{2}u^{2} + 2 t^{2}u^{2} - 4t^{4}u^{2} - 4t^{2}u^{4} \] \[ = 4t^{2}u^{2} - 4t^{4}u^{2} - 4t^{2}u^{4} + 4t^{4}u^{4} \] \[ \therefore s^{4} + t^{4} + u^{4} -2(s^{2}t^{2} + t^{2}u^{2} + u^{2}s^{2})+ 4s^{2}t^{2}u^{2} = 0. \]
This is much better, being nicely symmetrical between s, t and u. We can get it into a slightly more convenient form by noting that
\[ 2(s^{2}t^{2}+ t^{2}u^{2}+ u^{2}s^{2}) = (s^{2}+t^{2}+u^{2})^{2} - (s^{4}+t^{4}+u^{4})\; ; \]
then the equation becomes
\[ 2(s^{4}+t^{4}+u^{4}) - (s^{2}+t^{2}+u^{2})^{2} +4s^{2}t^{2}u^{2} = 0.\]
Substituting the expressions for s, t and u derived from the cosine rule, we obtain
\[ 2(\alpha^{2}\beta^{2} + \beta^{2}\gamma^{2} + \gamma^{2}\alpha^{2}) - (\alpha\beta+\beta\gamma+\gamma\alpha)^{2} + 4 \alpha^{2}\beta^{2}\gamma^{2} = 0. \]
Dividing through by $\alpha^{2}\beta^{2}\gamma^{2}$,
\[ (\frac{1}{\gamma} + \frac{1}{\alpha} + \frac{1}{\beta})^{2} = 2( \frac{1}{\gamma^{2}} + \frac{1}{\alpha^{2}} + \frac{1}{\beta^{2}} ) + 4. \]
Now
\[ \frac{1}{\alpha} = \frac{A}{a} = \frac{a+d}{a} = 1 + \frac{d}{a} \] \[ \frac{1}{\beta} = 1 + \frac{d}{b} \] \[ \frac{1}{\gamma} = 1 + \frac{d}{c} ; \]
and so, writing $\sigma$ for d/a + d/b + d/c, $\tau$ for (d/a)² + (d/b)² + (d/c)², our equation becomes
\[ (3 + \sigma)^{2} = 2(3+2\sigma+\tau) + 4 \] \[ \therefore 9 + 6\sigma + \sigma^{2} = 6 + 4\sigma + 2\tau + 4 \] \[ \therefore 2\tau = -1 + 2\sigma + \sigma^{2} = (\sigma+1)^{2} - 2 \] \[ \therefore 2(\tau+1) = (\sigma+1)^{2} \] \[ \therefore 2(1+\frac{{d}^{2}}{{a}^{2}}+\frac{{d}^{2}}{{b}^{2}}+\frac{{d}^{2}}{{c}^{2}}) = {\left(1+\frac{d}{a}+\frac{d}{b}+\frac{d}{c}\right)}^{2} \]
Dividing through by d², we get
\[ 2(\frac{1}{{d}^{2}}+\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}+\frac{1}{{c}^{2}}) = {\left(\frac{1}{d}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)}^{2} \]
and we are done◊